on or off.For SLP source file jc_ml_S1.slp
0.5:: s(X,p) :- p(X), p(X). 0.5:: s(X,q) :- q(X). 0.5:: p(a). 0.5:: p(b). 0.5:: q(a). 0.5:: q(b).
and data file jc_ml_S1_data.pl
frequencies([s(a,p)-4,s(a,q)-3,s(b,p)-2,s(b,q)-3]).
the call succeeds with the learned PPs
?- fam( [goal(s(_A,_B)),slp(jc_ml_S1),datafile('jc_ml_S1_data.pl'),final_pps(PPs)] ).
PPs = [0.6602,0.3398,0.5858,0.4142,0.5,0.5]
Options
- count(CountMeth=exact)
- CountMeth in {exact, store, sample};
- times(Tms=1000)
- only relevant with CountMeth=sample
- termin(TermList)
- currently TermList knows about the following terms
- interactive
- ask user if another iteration should be run
- iter(I)
- I is the number of iterations
- prm_e(E)
- parameter difference between iteration, that renders termination due to convergence of all parameters, between two iterations
- ll_e(L)
- likelihood convergence limit;
- goal(Goal)
- the top goal, defaults to an all vars version of data;
- pregoal(PreGoal)
- a goal that called only once, before experiments are run. The intuition is that PreGoal will partially instantiate Goal.
- data(Data)
- the data to use, overrides datafile/1. Data should be a list of Yield-Times pairs. (All Yields of Goal should be included in Data, even if that means some get Times = 0.)
- prior(Prior=none)
- the distribution to replace the probability labels with. By default prior is used, so input parameters are used as given in Slp source file. System also knows about uniform and random. Any other distribution should come in Prolog source file named Prior.pl and define Prior/3 predicate. First argument is a list of ranges (Beg-End) for each stochastic predicate in source file. Second argument, is the list of actual probability labels in source file. Finally, third argument should be instantiated to the list of labels according to Prior.
- datafile(DataFile=data.pl)
- the data file to use, default is
data.pl. DataFile should have either a number of atomic formulae or a single formula of the form :frequencies(Data). - complement(Complement=none)
- one of : none (with PrbSc = PrbTrue, the default), success (with PrbSc = 1 − PrbF ail), or quotient (with PrbSc = PrbT rue/(PrbT rue + PrbF ail)).
- setrand(SetRand=false)
- sets random seeds. SetRand = true sets the seeds to some random triplet
while the default value false, does not set them. Any other value for
SetRand is taken to be of the form
rand(S1,S2,S3)as expected by system predicate random of the supported prolog systems. - eps(Eps=0)
- the depth Epsilon. Sets the probability limit under which Pepl considers a path as a failed one.
- write_iterations(Wrt=all)
- indicates which set of parameters to output. Values for Wrt are: all, last and none.
- write_ll(Bool==true)
- takes a boolean argument, idicating where loglikelihoods should be printed or not.
- debug(Dbg=off)
- should be set to on or off. If on, various information about intermediate calculations will be printed.
- return(RetOpts=[])
- a list of return options. The terms RetOpts contain variables. These will be instantiated to the appropriate values signified by the name of each corresponding term. Recognised are, initial pps/1 for the initial parameters, final pps for the final/learned parameters, termin/1 for the terminating reason, ll/1 for the last loglikelyhood calculated, iter/1 for the number of iterations performed, and seeds/1 for the seeds used.
- keep_pl(KeepBool==false)
- if true, the temporary Prolog file that contains the translated SLP, is not deleted.
- exception(Handle=rerun)
- identifies the action to be taken if an exception is raised while running Fam. rerun means that the same Fam call is executed repeatedly. Any other value for Handle will cause execution to abort after printing the exception raised.
file(s). ., and ./slp/ while on SWI it also looks in,
pack(’pepl/slp/’).bibtex(Type,Key,Pairs) term of the same publication.
Produces all related publications on backtracking.date(Year,Month,Day)).
?- pepl_version(V,D). V = 2:3:0, D = date(2021, 5, 6).
?- sload_pe(coin). ?- seed_pe. ?- sample(coin(Flip)). Flip = head.
sample(Goal) is equivalent to sample(Goal,0,_Path,Succ,Prb) where Succ is not fail and Prb is not 0.
?- seed_pe. ?- sample(coin(Flip),0,Path,Succ,Prb). Flip = head, Path = [1], Prb = 0.5.
The probability with which refutations/branches are sampled are proportional to the probabilities on the clauses. That is, sampling replaces SLD resolution with stochastic resolution.
If you have packs: mlu, b_real and Real.
?- lib(mlu). ?- sload_pe(coin). ?- seed_pe. ?- mlu_sample( sample(coin(Side)), 100, Side, Freqs ), mlu_frequency_plot( Freqs, [interface(barplot),outputs([svg]),las=2] ). Freqs = [head-53, tail-47].
Produces file: real_plot.svg
which contains the barplot for 53 heads and 47 tails from 100 coin flipping experiments.
Note that sampling is distinct to calling a Goal for finding its refutations and total probabilities. Sampling always takes the most general form of Goal and also returns failure paths. The idea is that if the underlying SLP defines a unique probability space summing up to 1, then each branch is sampled proportionaly and failed branches are integral part of the space.
The above is particularly important if Goal is partially instantiated.
?- seed_pe. ?- sample(coin(tail)). false. ?- seed_pe. ?- sample(coin(head)). true. ?- seed_pe. ?- sample(coin(Flip)). Flip = head.
To demonstrate the inability of SLPs to operate over arbitrary length objects, check:
?- sload_pe(member3).
?- lib(mlu).
?- seed_pe.
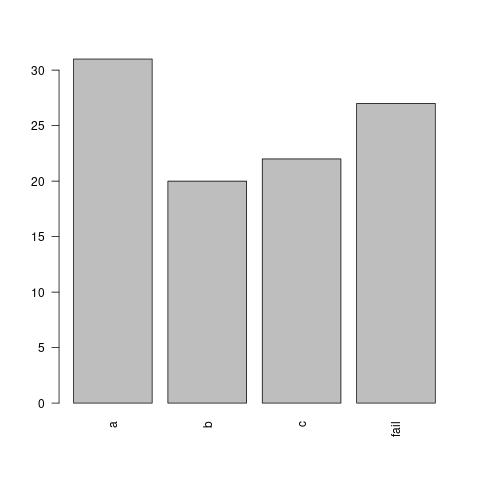
?- mlu_sample( sample(member3(X,[a,b,c])), 100, X, Freqs ),
mlu_frequency_plot( Freqs, [interface(barplot),outputs(png),stem('meb3from3'),las=2] ).
Freqs = [a-31, b-20, c-22, fail-27].
Produces file: meb3from3.png
...and:
?- lib(mlu).
?- sload_pe(member3).
?- seed_pe.
?- mlu_sample( sample(member3(X,[a,b,c,d,e,f,g,h])), 100, X, Freqs ),
mlu_frequency_plot( Freqs, [interface(barplot),outputs(png),stem('meb3from8'),las=2] ),
write( freqs(Freqs) ), nl.
freqs([a-34,b-16,c-22,d-5,e-9,f-6,fail-2,g-3,h-3])
Produces file: meb3from8.png
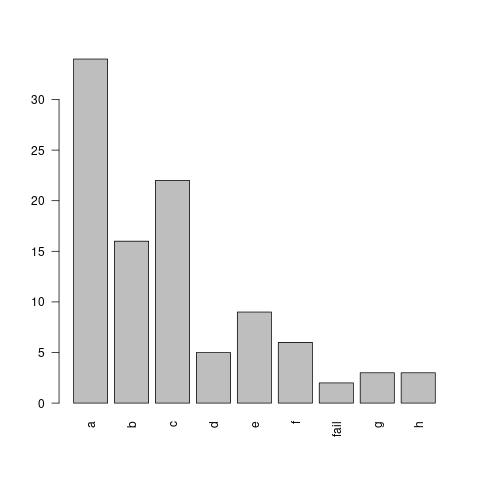
Eps is the epsilon value below which a derivation is considered a failure (prunes low probability branches).
Path is the arithmetic index of the clauses used in the derivation. Succ is bound to false if this was
a failure branch and is unbound otherwise. Prb is the probability of the sampled branch.
This predicate implements probabilistic sampling. Instead of SLD resolution we use the probabilistic labels to sample from the tree. There is no backtracing, and probabilistic failures will be returned.
?- sload_pe(coin). ?- seed_pe. ?- sample(coin(Flip),0,Path,Succ,Prb). Flip = head, Path = [1], Prb = 0.5.
The probability with which refutations/branches are sampled are proportional to the probabilities on the clauses. That is, sampling replaces SLD resolution with stochastic resolution.
Note that sampling is distinct to calling a Goal for finding its refutations and total probabilities. Sampling always takes the most general form of Goal and also returns failure paths. The idea is that if the underlying SLP defines a unique probability space summing up to 1, then each branch is sampled proportionaly and failed branches are integral part of the space.
The above is particularly important if Goal is partially instantiated.
?- seed_pe. ?- sample(coin(tail),0,Path,Succ,Prb). Path = [1], Succ = fail, Prb = 0.5. ?- seed_pe. ?- sample(coin(head),0,Path,Succ,Prb). Path = [1], Prb = 0.5 ?- seed_pe. ?- sample(coin(Flip),0,Path,Succ,Prb). Flip = head, Path = [1], Prb = 0.5.
?- sload_pe(coin). ?- seed_pe. ?- scall_sum( coin(Flip), Prb ). Prb = 1.0. ?- scall_sum( coin(head), Prb ). Prb = 0.5. ?- scall_sum( coin(tail), Prb ). Prb = 0.5.
A more complex example:
?- sload_pe(doubles). ?- scall_sum( doubles(head), Prb ). Prb = 0.25. ?- scall_sum( doubles(tail), Prb ). Prb = 0.25. ?- scall_sum( doubles(Side), Prb ). Prb = 0.5.
It also returns failed path probabilities. Instantiation is either the reserved token 'fail', or a term within Goal. If Goal is a single, variable, argument term, then the value of the variable is preserved. If Goal is of the form Left-Right, then Left is preserved and Right is expected to be the callable Goal, otherwise the whole of Goal is preserved.
The order in Pair are according to standard SLD resolution. The only special feature is that probabilistic failures are returned. There is no uniqueness on Instantion values.
?- sload_pe(doubles). ?- scall_findall( doubles(X), Pairs ). Freqs = [head-0.25, fail-0.25, fail-0.25, tail-0.25].
?- sload_pe(member3). ?- scall_findall( X-member3(X,[a,b,c]), Pairs ). Pairs = [a-1/3, b-0.2222222222222222, c-0.14814814814814814, fail-0.09876543209876543, fail-0.19753086419753085].
This uses standard SLD resolution so the order is as per Prolog. Failure paths are ignored here.
?- sload_pe(coin). ?- scall(coin(Flip)). Flip = head ; Flip = tail. ?- sload_pe(doubles). ?- scall(doubles(X)). X = head ; X = tail.
Compare to
?- scall_findall( doubles(X), Pairs ). Pairs = [head-0.25, fail-0.25, fail-0.25, tail-0.25].
Succeeds for all instantiations for which stochastic Goal has a successful derivation, with Prb being the product of all probabilitic labels seen on the way.
This uses standard SLD resolution so the order is as per Prolog. Failure paths are ignored here.
?- sload_pe(coin). ?- scall( coin(Flip), Prb ). Flip = head, Prb = 0.5 ; Flip = tail, Prb = 0.5. ?- scall( coin(head), Prb ). Prb = 0.5 ; false. ?- scall( coin(tail), Prb ). Prb = 0.5.
Also,
?- scall( doubles(X), Prb ). X = head, Prb = 0.25 ; X = tail, Prb = 0.25.
Compare to
?- scall_findall( doubles(X), Pairs ). Pairs = [head-0.25, fail-0.25, fail-0.25, tail-0.25].
This predicate is for people interested in the iternals of pepl. Use at your own peril.
The predicate arguments are as follows.
- The vanilla prolog Goal to call.
- The value of Eps(ilon) at which branches are to be considered as failures.
- The Path of a derivation
- A flag idicating a Succ(essful) derivation or otherwise. Succ is bound to the atom fail if this was a failed derivation and remains unbound otherwise.
- BrPrb the branch probability of the derivation.
?- sload_pe(coin). ?- seed_pe. ?- scall(coin(Flip), 0, sample, Path, Succ, Prb ). Flip = head, Path = [1], Prb = 0.5.
... or to backtrack overall paths
?- scall(coin(Flip), 0, all, Path, Succ, Prb ). Flip = head, Path = [1], Prb = 0.5 ; Flip = tail, Path = [2], Prb = 0.5.
A convenience predicate for running the examples from a common starting point for the random seed.
Specifically it unfolds to
?- set_random(seed(101)).
?- sload_pe(coin). ?- seed_pe. ?- sample(coin(Flip)). Flip = head. ?- set_random(seed(101)). ?- sample(coin(Flip)). Flip = head. ?- sample(coin(Flip)). Flip = tail.